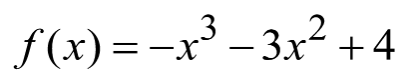Polynomial Functions Reflection Activity              

 

Common Core Standards

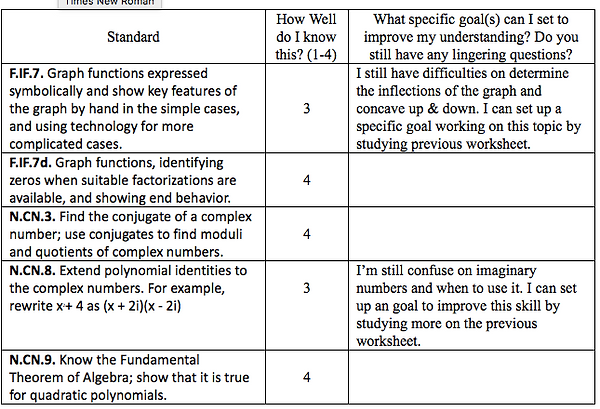
F.IF.7. Graph functions expressed symbolically and show key features of the graph by hand in the simple cases, and using technology for more complicated cases.

F.IF.7d. Graph functions, identifying zeros when suitable factorizations are available, and showing end behavior.

N.CN.3. Find the conjugate of a complex number; use conjugates to find moduli and quotients of complex numbers.

N.CN.8. Extend polynomial identities to the complex numbers. For example, rewrite x2+ 4 as (x + 2i)(x - 2i)

N.CN.9. Know the Fundamental Theorem of Algebra; show that it is true for quadratic polynomials.

 

 

 

 

 

 

 

 

 

 

Given the numerical, algebraic, and graphical representations of the polynomial functions below, state as many facts as you possibly can about each of the three different functions. As you do this, reflect upon the standards covered in the Polynomial Functions Unit and form a plan on how you can improve.

 

 

 

 

 

 

-Determine where it pass through the x axis (2,0)

-Knowing where the lines are below or above the x axis.

-The intercept is 2

-The graph increase from both ends

-Determine the zeros

 

-Using the constant term and the coefficient to determine the possible roots.

-The intercept is 4

-The coefficient is -1

-The highest degree of this equation is 3, so there will be 3 zeros in total.

-The graph increases to the left end but decreases to the right end.

-The graph does not pass the zero.

-Factor the equation out to find how many times is x=0, but in this equation there’s no x=0.

-Use Descartes’s Rule of Signs to help determine the possible combinations of positive, negative,zero, and imaginary roots that the function can have.

-There is only one positive.

-There are 2 negatives.

A negative correlation demonstrates a connection between two variables in the same way a positive correlation coefficient does, and the relative strengths are the same.

-cubic function

 

Graph of h(x)

-The intercept is 3.

-The multicities of (x+4) is 2.

-The multicities of (x-1) is 1

-The multicities of (x-3) is 1

-The function of this graph represents a quadratic with 4 multicities.

-There are 3 zeros on the x axis.

-The graph increases on both ends.

-There are 2 inflections.

 

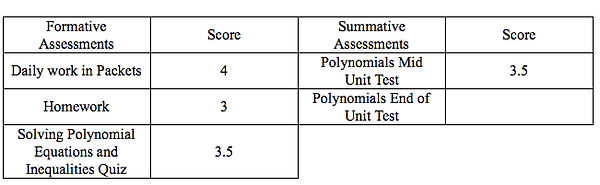
Student Improvement Plan

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

How Well do I know this? (1-4)

 

1. I am still unfamiliar with this concept.
2. I remember this but need to learn more. 
3. I am fairly confident in my knowledge of this and can implement this on my own.
4. I am confident in my knowledge of this and could teach it to someone else.